Analysis of a "Plaiting Scheme"

zur Seite in deutscher Sprache:

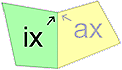Consider a set of 6 congruent paper strips I, II, III, IV, V, and VI each consisting of 4 outer quadrilaterals a1, a2, a3, a4 and 4 inner quadrilaterals i1, i2, i3, i4. Inner- and outer quadrilaterals alternate, and every paper strip starts with an inner quadrilateral i1. All neighbouring quadrilaterals ix und ax are provided with an orientation as shown. The paper strips are plaited together, using the following table:

	a1	a2	a3	a4
I	↑↑ i3 IV	↑↑ i2 II	↑↑ i1 III	↑↑ i4 VI
II	↑↑ i1 V	↑↑ i2 III	↑↑ i1 I	↑↑ i2 IV
III	↑↑ i1 VI	↑↑ i2 I	↑↑ i1 II	↑↑ i4 V
IV	↑↑ i3 VI	↑↑ i2 V	↑↑ i3 II	↑↑ i4 I
V	↑↑ i3 III	↑↑ i4 II	↑↑ i1 IV	↑↑ i2 VI
VI	↑↑ i3 I	↑↑ i4 III	↑↑ i3 V	↑↑ i4 IV

Here e.g. a2 III ↑↑ i2 I means, that during plaiting the inner quadrilateral i2 of paper strip I has to be brought upon the outer quadrilateral a2 of paper strip III, such that the orientation arrows of both quadrilaterals have equal direction.
The condition, that the paper strips are pairwise congruent, implies together with the shown "plaiting table", that two sets of equal oriented congruent quadrilaterals appear on the paper strips, namely: {i1, i3, a1, a3} and {i2, i4, a2 a4}. It turns out, that a single paper strip has the following shape:
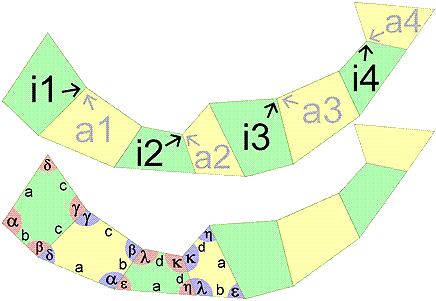The edges a, b, c, and d and the angles α, β, γ, δ, ε, η, κ, and λ have to be choosen within certain borders. Especially the following conditions for the angles must hold:
γ ≤ 120^o,
κ ≤ 120^o,
β + δ + η + λ ≤ 360^o,
α + ε ≤ 180^oThese inequalities result from the fact, that caused by plaiting the paper strips, certain angles meet in a vertex of the plaited solid and therefore their sum cannot exceed 360^o. The resulting plaited polyhredron in fact has 26 points ("vertices"), where the following angles (see table) meet together:

1: α(a1 I), ε(a2 IV), α(a1 V), ε(a2 III)	2: β(a1 I), λ(a2 III), η(a2 II), δ(a3 IV)	3: γ(a1 I), γ(a3 IV), γ(a3 II)	4: δ(a1 I), β(a3 II); λ(a2 V), η(a2 IV)
5: ε(a2 I), α(a1 II), ε(a4 V), α(a1 VI)	6: η(a2 I), δ(a1 VI), β(a1 III); λ(a2 II)	7: κ(a2 I), κ(a2 II), κ(a2 III)	8: λ(a2 I), η(a2 III), δ(a1 V), β(a1 II)
9: α(a3 I), ε(a4 III), α(a3 V), ε(a4 IV)	10: β(a3 I), λ(a4 IV), η(a4 VI), δ(a1 III)	11: γ(a3 I), γ(a1 III), γ(a1 VI)	12: δ(a3 I), β(a1 VI); λ(a4 V), η(a4 III)
13: ε(a4 I), α(a3 VI), ε(a2 V), α(a3 II)	14: η(a4 I), δ(a3 II), β(a3 IV); λ(a4 VI)	15: κ(a4 I), κ(a4 IV), κ(a4 VI)	16: λ(a4 I), η(a4 IV), δ(a3 V), β(a3 VI)
17: γ(a1 II), γ(a1 V), γ(a3 III)	18: δ(a1 II), β(a3 III); λ(a2 VI), η(a2 V)	19: ε(a2 II), α(a1 III), ε(a4 VI), α(a3 IV)	20: ε(a4 II), α(a1 IV), ε(a2 VI), α(a3 III)
21: η(a4 II), δ(a3 III), β(a1 V); λ(a2 IV)	22: κ(a4 II), κ(a2 IV), κ(a2 V)	23: λ(a4 II), η(a2 V), δ(a3 VI), β(a1 IV)	24: κ(a4 III), κ(a4 V), κ(a2 VI)
25: λ(a4 III), η(a2 VI), δ(a1 IV), β(a3 V)	26: γ(a1 IV), γ(a3 VI), γ(a3 V)

At most there arise 48 sides for the plaited solid, in this case the paper strips necessarily have to be folded along all quadrilateral edges crossing the strip and, additionally, for every quadrilateral along a certain diagonal.
The symmetry group of the solid consists of 12 elements at least, because the outer quadrilateral a1 of paper strip I can be mapped onto the outer quadrilaterals a1 or a3 of any of the 6 strips.
When the quantities b, c and d and the angles α, . . . , λ are chosen properly, then paper strips for plaiting can be produced not only for all 5 Platonic Solids, but also for the cuboctahedron, the deltoid-icosahedron and the disdyakis-dodecahedron. In details:

Tetrahedron d = c = b = a α = γ = ε = κ = 120o β = δ = η = λ = 60o folding lines: the diagonals with arrows of i2, a2, i4, and a4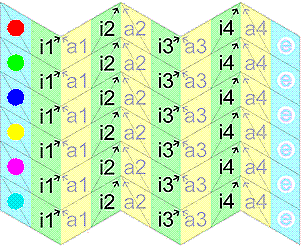

pattern download: 2593 x 2105 pix, 315 kb: tr6.gif

back ...             ... to be continued ...            (last update: 2007/October/27)